Data
Charting Data
A simple way to chart data in GS Quant is by installing matplotlib. This plotting library can be
used to easily generate plots, histograms, power spectra, bar charts, error charts, scatter plots,
etc.
Let's use this library to chart calculated implied volatility from GS Quant.
Note
Examples require an initialized GsSession and data subscription. Please refer to Sessions for details.
Querying Data
First, let's retrieve S&P 500 end of day implied volatility for 1 month tenor with forward strike:
from gs_quant.data import Dataset
from gs_quant.markets import PricingContext
market_date = PricingContext.current.market.date # Determine current market date
vol_dataset = Dataset(Dataset.GS.EDRVOL_PERCENT_STANDARD) # Initialize the equity implied volatility dataset
vol_data = vol_dataset.get_data(market_date, market_date, ticker='SPX', tenor='1m', strikeReference='forward')
print(vol_data.tail())Output:
absoluteStrike assetId ... ticker updateTime
21 4049.365704 MA4B66MW5E27U8P32SB ... SPX 2019-06-17T22:18:01Z
22 4193.985908 MA4B66MW5E27U8P32SB ... SPX 2019-06-17T22:18:01Z
23 4338.606111 MA4B66MW5E27U8P32SB ... SPX 2019-06-17T22:18:01Z
24 5061.707130 MA4B66MW5E27U8P32SB ... SPX 2019-06-17T22:18:01Z
25 5784.808149 MA4B66MW5E27U8P32SB ... SPX 2019-06-17T22:18:01Z
[5 rows x 9 columns]Charting Data
Implied Volatility By Strike
Now, let's use vol_data to chart the implied volatility by relative strike:
Note
Remember to install matplotlib.
add the following import statement to have matplot available:
import matplotlib.pyplot as pltthen plot your data like so:
strikes = vol_data['relativeStrike']
vols = vol_data['impliedVolatility'] * 100
plt.plot(strikes, vols, label='Implied Volatility by Strike')
plt.xlabel('Relative Strike')
plt.ylabel('Implied Volatility')
plt.title('Implied Volatility by Strike')
plt.show()Which will create a plot like this:
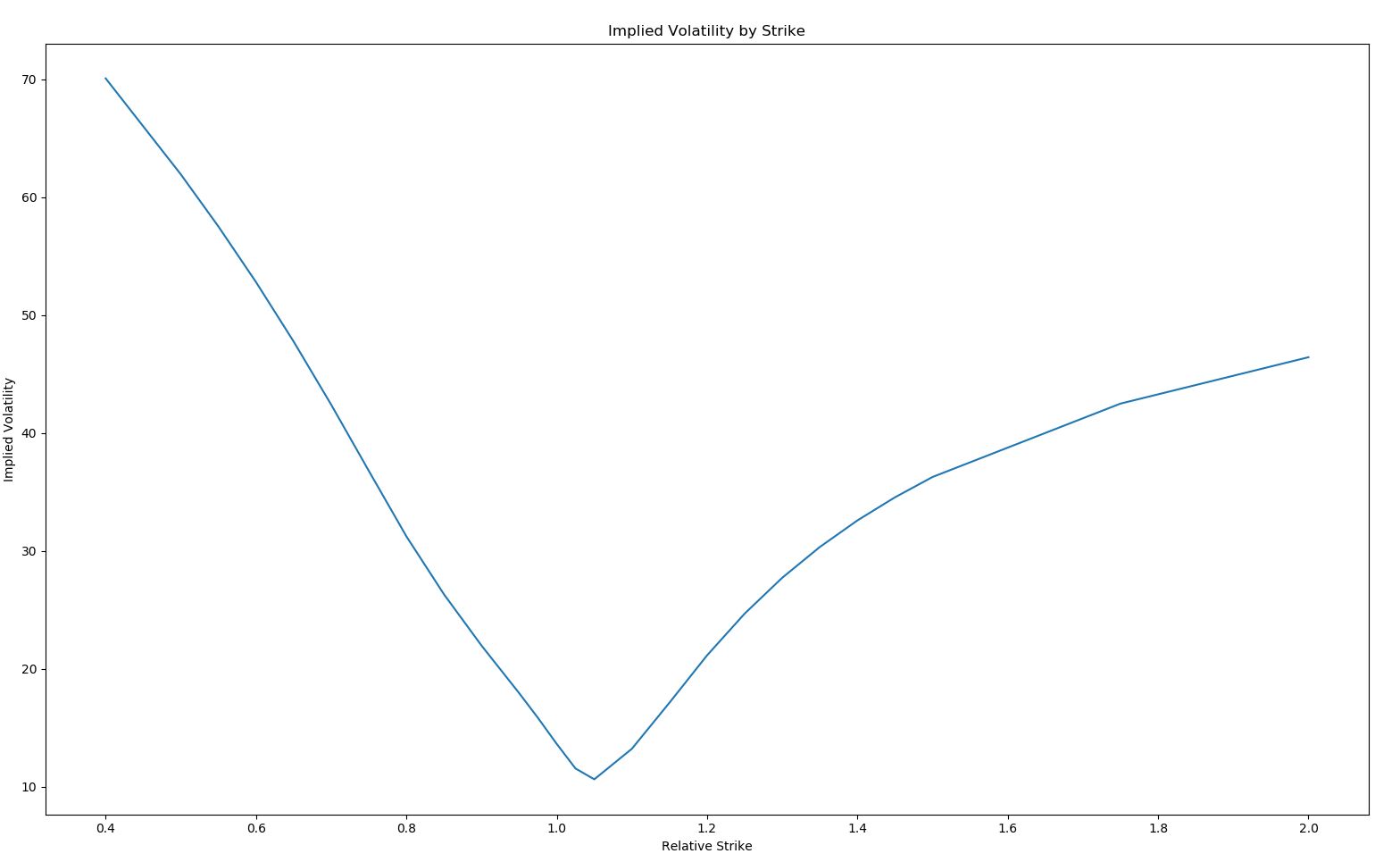
Implied Volatility By Tenor
Likewise we can use the same technique to chart the implied volatility by tenor:
from gs_quant.timeseries.measures import _to_offset
vol_data = vol_dataset.get_data(market_date, market_date, ticker='SPX', relativeStrike=1.0, strikeReference='forward')
# Create a new column converting relative dates to actual date times
vol_data.loc[:, 'tenorDate'] = vol_data.index + vol_data['tenor'].map(_to_offset)
# Sort the data frame by the newly created column
vol_data = vol_data.sort_values(by=['tenorDate'])
tenors = vol_data['tenor']
vols = vol_data['impliedVolatility'] * 100
plt.plot(tenors, vols, label='Implied Volatility by Tenor')
plt.xlabel('Tenor')
plt.ylabel('Implied Volatility')
plt.title('Implied Volatility by Tenor')
plt.show()Producing:
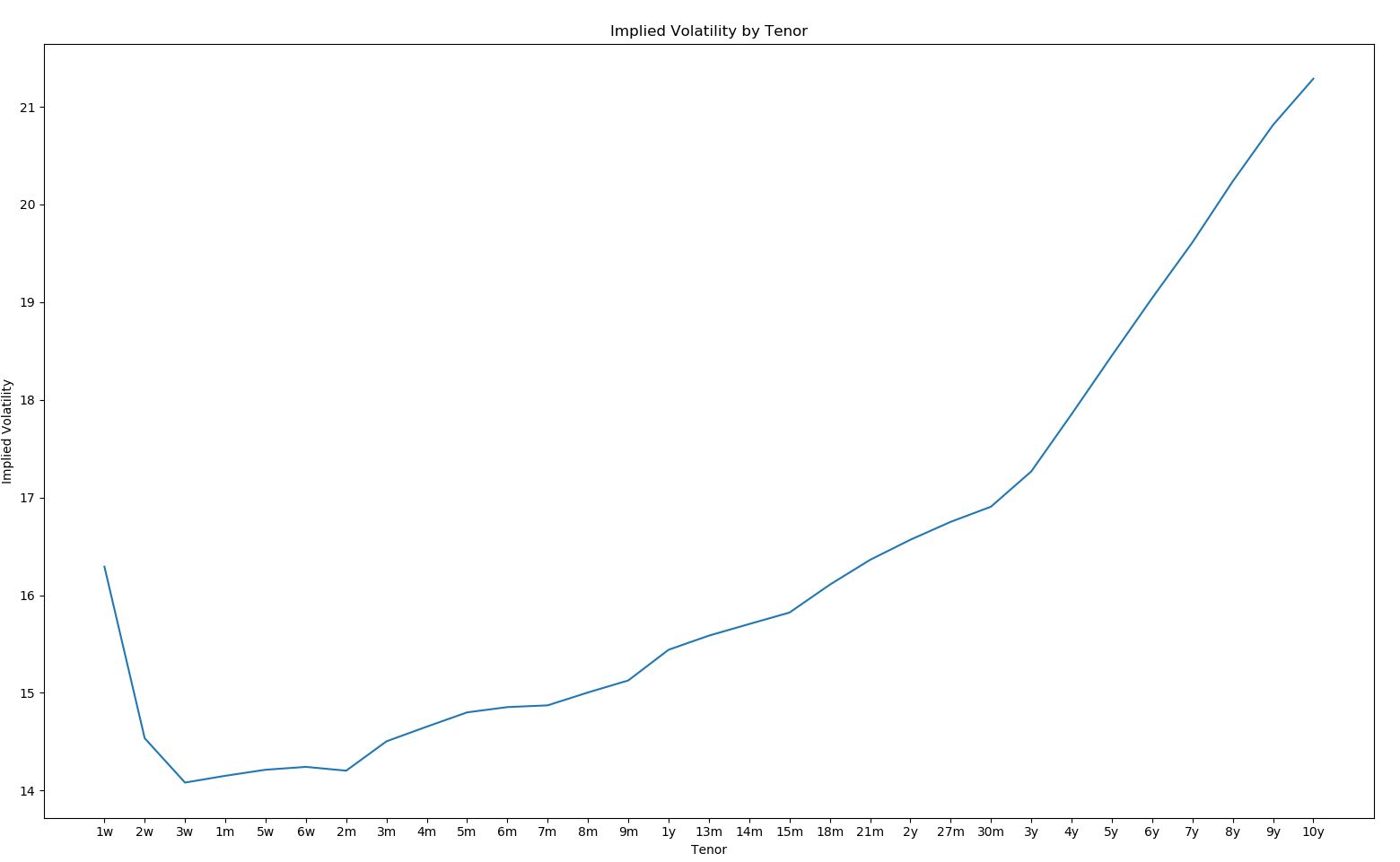
Implied Volatility Area By Tenor And Strike
Now, let's combine the two and plot a vol surface to chart the implied volatility by tenor and strike:
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from gs_quant.data import Dataset
from gs_quant.datetime import point_sort_order
from gs_quant.markets import PricingContext
# Initialize the dataset for equity implied volatility
vol_dataset = Dataset(Dataset.GS.EDRVOL_PERCENT_STANDARD)
market_date = PricingContext.current.market.date
tenors_to_plot = ["2w", "1m", "2m", "3m", "4m", "5m", "6m", "9m", "1y"]
fig = plt.figure(figsize=(16, 9))
ax = fig.add_subplot(111, projection='3d')
# Implied vol data for the current market data date
vol_data = vol_dataset.get_data(market_date, market_date, ticker='SPX', strikeReference='forward')
vol_data = vol_data[vol_data.tenor.isin(tenors_to_plot)]
vol_data['tenorDays'] = vol_data.tenor.map(lambda t: point_sort_order(t))
# Reformat the data
X = vol_data.relativeStrike.unique()
Y = vol_data.tenorDays.unique()
Z = np.array([vol_data[vol_data.tenorDays == y].impliedVolatility.values.tolist() for y in Y]) * 100
X, Y = np.meshgrid(X, Y)
# Plot the surface
ax.xaxis.set_label_text("Strike")
ax.yaxis.set_label_text("Tenor")
ax.zaxis.set_label_text("Implied Vol")
ax.set_zlim(0, 75)
ax.set_yticks(vol_data.tenorDays.unique())
ax.set_yticklabels(vol_data.tenor.unique())
surface = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm, linewidth=0, antialiased=False)
plt.show()The previous example should produce a 3D graph similar to this:
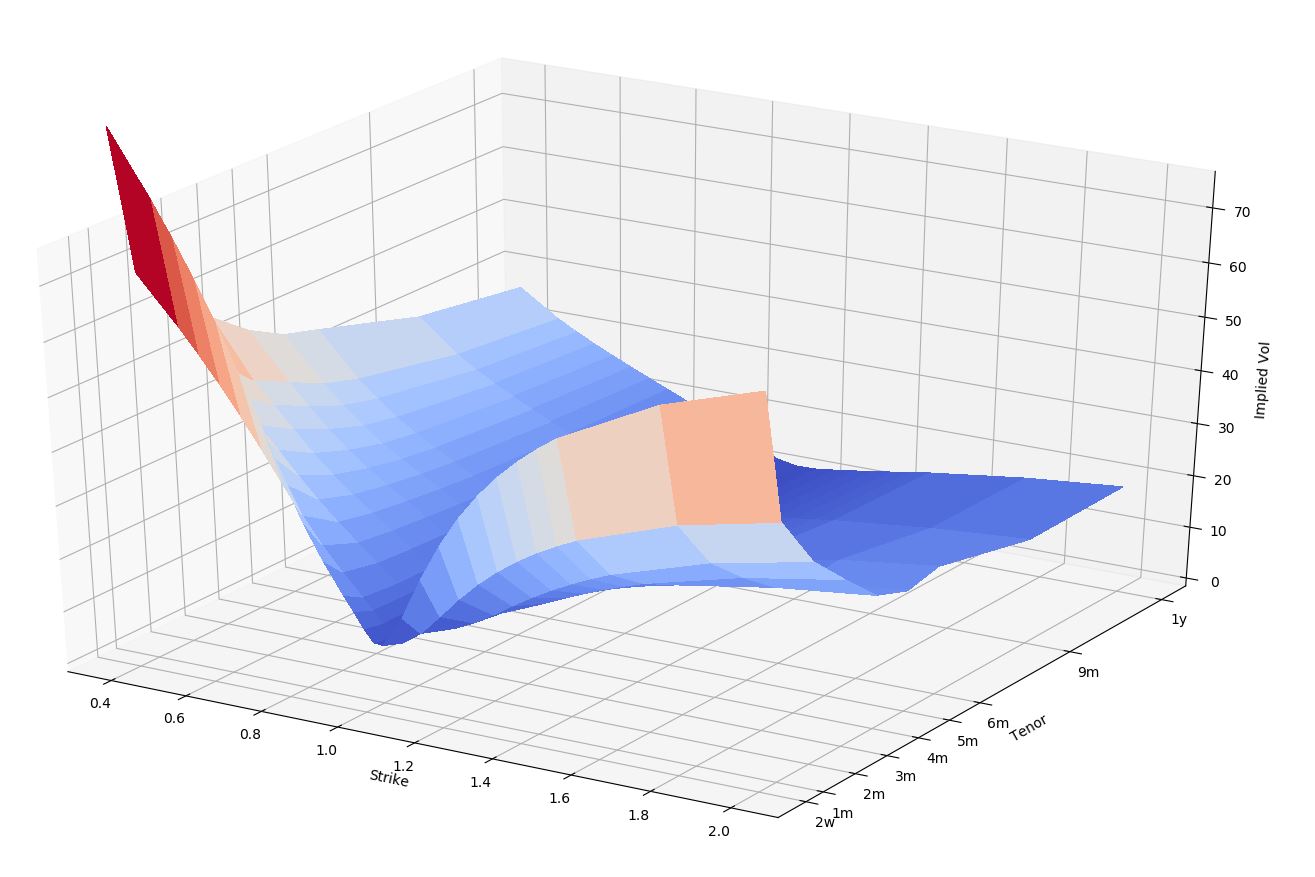
Related Content
Exporting Data
arrow_forwardWas this page useful?
Give feedback to help us improve developer.gs.com and serve you better.